In each spectroscopic observation, we will devote between one-tenth and one-sixth of the fibers to a survey of quasar candidates. These are defined as stellar objects with colors well separated from the stellar locus.
The cumulative quasar counts in pi steradians as a function of B magnitude are given in Table 3.3.1. The data are based on the results of Crampton, Cowley, and Hartwick (1987; cf., La Franca and Christiani 1996). Quasars on our system have g' ~ B - 0.3 , but the transformation is affected at the level of several tenths of a magnitude at different redshifts by the emission lines. We give approximate g' values in the table.
| B | g' | N(<B) |
|---|---|---|
| 16 | 15.7 | 100 |
| 17 | 16.7 | 1300 |
| 18 | 17.7 | 11300 |
| 19 | 18.7 | 52900 |
| 20 | 19.7 | 172000 |
| 21 | 20.7 | 414000 |
The proposed instrumentation of the Sloan Digital Sky Survey will therefore allow detailed study of the order of 100,000 quasars brighter than g' ~ 19.7 . For comparison, the largest samples of quasars from individual surveys compiled in the last decade (cf., Hartwick and Schade 1990; La Franca and Christiani 1996, for reviews) include the works of Boyle, Shanks, and Peterson (1988) (423 quasars with z < 2.2), Hewett, Foltz, and Chaffee (1995) (1055 quasars with z < 3.4), Warren et al. (1991a,b, 1994) (85 quasars with 2.2 < z < 4.5), Schneider, Schmidt, and Gunn (1994) (140 quasars with 2.1 < z < 4.8), Christiani et al. (1995) and La Franca and Christiani (1996) (327 quasars with z < 2.2 ). The large, well-defined data base produced by the SDSS can be used to address many pressing questions concerning the nature of quasars, their evolution, quasar clustering, galaxy formation at high redshifts, and the properties of the intergalactic medium.
The SDSS will use the colors and morphology of objects to identify quasar candidates in the photometric data. There have been several successful "multicolor" surveys for quasars based on photographic material, for example the programs described by Koo and Kron (1988), Boyle, Shanks, and Peterson (1988), and Warren et al. (1991a,b, 1994). The last project, using six broad bands ranging from u to i , discovered over 100 quasars (85 in the complete sample), including the first object with a redshift larger than four (Warren et al. 1987). The quasar with the highest known redshift ( z = 4.90) was found in a multicolor survey using drift-scanning CCDs (Schneider, Schmidt, and Gunn 1991b).
The proposed quasar selection scheme for the SDSS is quite similar to previous studies; objects of stellar appearance with colors that lie well outside the stellar locus will be flagged for spectroscopic investigation. The SDSS will have several improvements (besides areal coverage) over previous multicolor quasar surveys. The survey data base is produced by CCDs, with their associated advantages (linear response, photometric accuracy, better sky subtraction) over photographic material. The colors for each object are measured virtually simultaneously, so source variability will not be a confusing factor. The wavelength coverage of the SDSS filter set (3540 Å < lambda < 9240 Å) has been matched by one previous CCD survey (Hall et al. 1996a,b), but this was over a very limited area of sky. The reddest bands in particular will permit identification of quasars with redshifts as high as six and possibly seven!
Multicolor surveys, while a very successful method for finding quasars, do present some technical challenges. The fundamental basis for identifying quasars in such programs is the difference between the spectral energy distributions (SEDs) of quasars and stars. To a large degree the SEDs of individual quasars show the same features: a smooth, roughly power-law continuum and a number of broad emission lines of certain ions. There are, however, significant variations in the values of the slopes of the power law, and in the strengths and widths of the emission lines. Quasar continua are strongly affected by absorption from the Lyman alpha forest, as well as Lyman limit systems. In addition, the spectra of a small fraction (5% - 10%) of quasars possess strong, broad absorption features (the Broad Absorption Line, or BAL quasars; see section 3.3.4 h ). A further complication is that the survey colors of a given quasar SED depend on the redshift of the object. The Warren et al. (1994) paper presents an excellent discussion of the technical challenges of quasar detection in multicolor surveys.
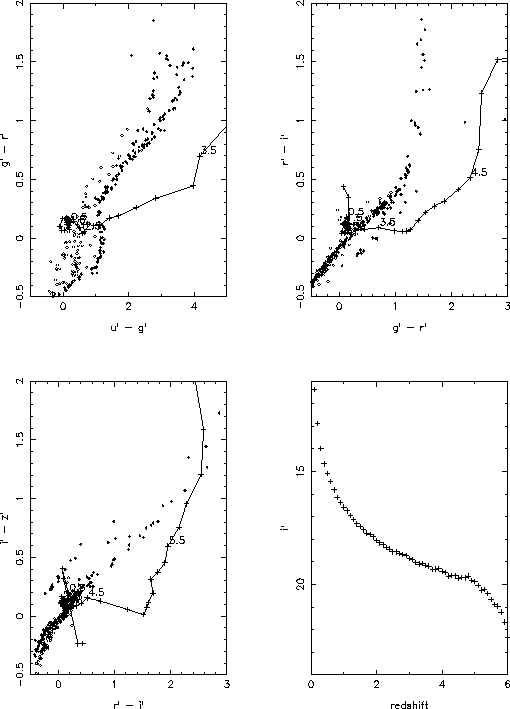
The colors in the SDSS filter system of model quasars. The plot shows the median track from a Monte Carlo simulation of quasar spectra as a function of redshift. The filled circles are the colors of stars from the atlas of Gunn and Stryker (1983), the open circles are white dwarfs from Greenstein and Liebert (1990). The panel in the lower right is the i' magnitude as a function of redshift of a quasar with the luminosity of 3C273.
We illustrate the nature of the SDSS quasar identification problem with Figure 3.3.1, which shows the locations of the expected quasar tracks in the color-color diagrams as a function of redshift for the SDSS filter system. The quasar tracks used are the median tracks of a Monte-Carlo simulation of quasar colors in the SDSS filter system. The emission spectra of quasars are simulated according to observed distributions of the power law continuum (alpha=0.5+-0.3, Francis 1996) and a total of 36 emission lines and FeII features. The absorption features include Lyman alpha forest and Lyman Limit System (LLS) absorption simulated according to the procedures of Moller and Jakobsen (1990). The upper two and lower left panels display the results for the three sets of adjacent color pairs. The filled circles represent the stars contained in the spectrophotometric atlas of Gunn and Stryker (1983); the open circles are the white dwarfs studied by Greenstein and Liebert (1990). The relative density of star points in these figures does not reflect the expected relative density of objects in the survey, nor the effect of photometric errors. In particular, the number density of hot main sequence stars is strongly over-represented in these plots, especially at high galactic latitudes; we have simply plotted all of the objects in the two catalogs to show the positions of known stellar types.
Magnitudes in the SDSS system of the quasar tracks are marked with plusses at intervals of 0.1 in redshift. The graph in the lower right is the mean i' magnitude of a quasar with the absolute magnitude of 3C 273 ( V = -27 ). Such a quasar is brighter than 20th magnitude in the i' band out to a redshift of about five.
Figure 3.3.1 shows the general characteristics of the quasar/star separation problem for SDSS, but one should keep in mind that: 1. the quasar positions in color space, especially for those of high redshift, have a big dispersion, which is mainly due to the distribution of absorbers in the line of sight; 2. the statistics of the Lyman alpha and Lyman Limit absorptions used in the simulation are based on observations of quasars with redshifts smaller than 4.5 (Figure 3.3.7), while the colors of quasars of redshifts larger than this are based on the extrapolation of the absorption to higher redshift; 3. emission line compact galaxies, which are one of the principal contaminants in multicolor QSO surveys (Hall et al. 1996a) are not included in these plots. Some of these have very strong H- alpha and [OIII] emission, and have similar colors to quasars.
The quasar tracks in Figure 3.3.1 reveal the overall features of their color distributions : 1. little change in the colors at low redshifts as a succession of relatively weak emission lines marches through the filters; 2) a move to the left (blue) in the diagrams when the Lyman alpha emission line enters the bluest of the three filters represented in each diagram; 3) a large shift to the right (red) as the Lyman alpha emission enters the middle filter and the absorption is seen by the blue filter; 4) eventually, when the optically-thick LLS absorption begins to show up in the bluest filter, the majority of the radiation will be absorbed by the LLS, and quasars become undetectable in those filters. As a result, their colors will be very different from those of any stars or low-redshift compact galaxies.
At redshifts smaller than 2.1, the u' filter measurements are crucial for separating the colors of quasars and stars. The ultraviolet measurement places quasars well away from main-sequence stars (these stars have a strong Balmer jump not present in quasars; the main problem is confusion of the quasars with white dwarfs; cf., Green, Schmidt and Liebert 1986). Employing 5 colors will help in separating them, since the Rayleigh-Jeans tail of a black body (fnu~ nu² ) is very different from the quasar power law (fnu~nu-0.5). At redshifts larger than 2.5, the u' filter is no longer a good quasar/star discriminant; once Lyman alpha enters the g' filter, the quasar enters the realm of the main-sequence stars, and have very similar colors to the F-type stars (this is analogous to the z = 2.2 limit for UVX surveys).
The main place where quasars are difficult to separate from stars lies in the range z = 2.5 - 3.0. This is a common feature for all broad-band multicolor surveys, since in this redshift range, the three spectral features of quasars, i.e. absorption due to the Lyman alpha forest, Lyman alpha emission and the power law continuum redward of Lyman alpha , are redshifted to approximately the positions of three features prominent in F-type stars: the Balmer jump, the maximum in the stellar continuum and the gradual decline after that. The large width of the broad-band filters smooths these features and gives quasars and F type stars very similar colors. The selection effects in this range are strong and quite dependent on the number density of F-G stars in the observed direction. An accurate estimate of the quasar density in this redshift range needs detailed modelling of the distribution of quasars and stars in color space. The only way to tie this down observationally is a complete survey of all stellar objects over some limited area of sky. As discussion in Section 5.5, we plan to do exactly this in the Southern stripe.
When the redshift is greater than 3.5, the existence of LLS in quasar spectra makes them rather easy to distinguish from stars. The APM survey (Storrie-Lombardi et al. 1996) and the DPOSS survey (Kennefick et al. 1996) use broad-band colors to successfully find high redshift quasars. The SDSS color system also has no problem in separating quasars from stars in this regime, as we saw above.
A detailed study of the distribution of point-like sources in the color space, including a detailed Galactic model to simulate the distributions of stars and white dwarfs, and a quasar distribution based on the known quasar luminosity function is currently underway. Figure 3.3.2 shows work in progress along these lines by Xiaohui Fan, a graduate student at Princeton University. This is a model color-color-color diagram ( u' - g' vertically, g' - r' horizontally, r' - i' into the page) of stellar objects brighter than r' = 20 that would be seen at the North Galactic pole. The distribution of objects in three dimensions is shown in the center, and the projection onto each of the principal two-dimensional planes is shown on the edges. The red dots are stars, using the stellar population models and colors of Ng (1994). Notice that unlike the color-color diagrams of the previous figure, the hottest stars are simply not present: there are very few stars earlier than F towards the poles! The blue points represent quasars; the vast majority of them are beyond the blue end of the stellar locus, representing the fact that blue quasars with z < 2.5 are much more common than higher-redshift, and therefore redder, quasars. The green points are white dwarfs, with colors from the simulations of Bergeron (private communication), and with mass distribution and luminosity function from Liebert et al. (1988). Photometric errors have been included in this diagram. This work is far from complete: among other things, we do not model the presence of compact emission-line galaxies, binary stars, the reddest stars, and other important contaminants. However, these diagrams will be invaluable as we develop our quasar selection criteria.
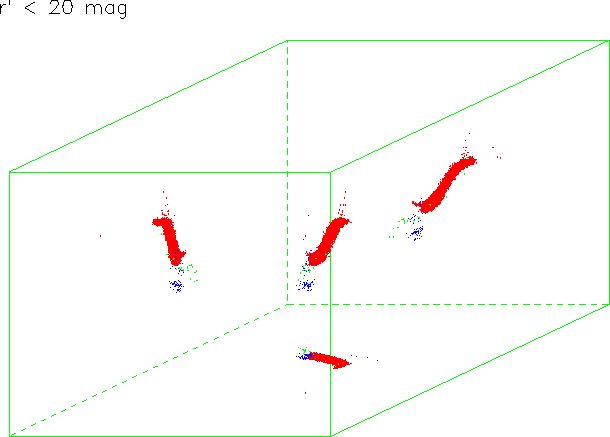
Color-color-color diagram for stars in the NGP region. The plots show ( u' - g' vertically, g' - r' horizontally, and r' - i' into the page). The three-dimensional distribution is shown in the center, with projections on the three planes on the sides. Red points are stars, green points are white dwarfs, and blue points are quasars. Photometric errors are included in this figure.
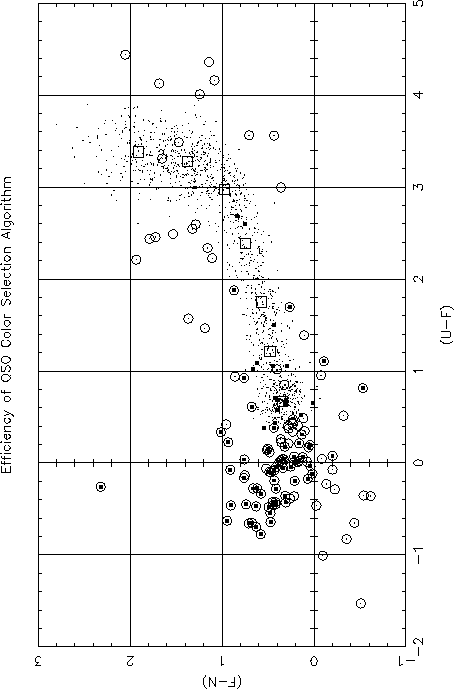
Fit of the stellar locus (open squares) in color space. The data are from Trevese et al. (1994). Known stars are dots and quasars are filled squares. Sources that were chosen as quasar candidates are circled.
An ideal quasar selection algorithm would be (a) uniform over the survey area, such that the quasar population in different regions of the sky can be compared directly (b) complete, in that quasars of all types are included, and (c) efficient, in that the number of non-quasars targeted is minimized. These three requirements pull us in different directions, given the changing stellar densities and populations as a function of direction, and the presence of quasars with broad-band colors essentially indistinguishable from stars. We thus cannot simultaneously optimize all three. Our approach is to enforce the uniformity requirement over only half of the survey area, and not require 100% completeness (which would be impossible anyway) over the entire survey area. As mentioned above, the completeness of the quasar sample will be quantified with the parallel survey of every stellar object over an appreciable region in the Southern stripe (Section 5.5).
Based on these simulations and data, and with these requirements in mind, the SDSS quasar working group has developed an algorithm to select quasars from the point-source objects found in the photometric observations. The scatter of stars around the mean stellar locus in color-color-color-color space is modelled as a Gaussian distribution with width varying as a function of position along the locus; quasars are defined as outliers from this distribution. In order that the quasar selection be uniform, we require that the stellar locus and its scatter be defined a priori; this is a major task of the test year. The stellar population, and the stellar density itself, of course varies strongly as a function of direction. For this reason, the quasar survey will be done in two parts. A uniform and deep survey of quasars will be done in the "cap" region, the half of the survey area at lowest stellar density according to the star-count models of Bahcall and Soneira (1981). This would account for roughly 75% of the quasar candidates surveyed over the sky. In the "skirt", the increased stellar density would mean that the number of false positives would become prohibitively high (especially considering that the changing stellar population will cause the stellar locus to move), and thus we back off and select only the brightest candidates with the highest statistical confidence of being quasars. In both cap and skirt, stellar objects associated with radio sources from the FIRST survey (Becker et al. 1995) will be targeted independent of their colors; estimates are that this will represent between 5 and 10 extra fibers per plate. The details of the quasar selection are still very much under development, and indeed refining the quasar selection criteria will be the most important and time-consuming job of the test year (Section 5.3). Our aim is for roughly 70% efficiency, and thus we plan to target of the order of 140,000 quasar candidates to get 100,000 bona fide quasars, again the bulk of them in the low stellar density pi /2 ster of the survey footprint. The quasar counts in Table 3.3.1 imply that a g' limit of roughly 19.7 is appropriate, but this will need to be carefully calibrated during the test year, and of course this will need to be augmented with additional selection in the redder bands for those quasars whose redshifts put Lyman alpha beyond the g' band.
As an illustration, the prototype algorithm has been tested using a set of UJFN magnitudes and object identifications from the SA 57 survey of Trevese et al. (1994). Selection of objects which lie more than 3 sigma from the stellar locus (note that the "thickness" of the stellar locus is a function of color) yielded 79% completeness with 47% contamination, as shown in Figure 3.3.3. Much of the contamination is due to white dwarfs (lower-left-hand corner of the plot), and as mentioned above, we can reduce this contamination considerably by use of all the color information at our disposal. The contamination should be further reduced with the smaller photometric errors the SDSS data will have, and reduced further still by not including objects in regions of color-color space in which quasars are very rarely found (although this will unfortunately reject some fraction of the rare quasars with very unusual SEDs; cf., Section 3.3.4i).
The use of the FIRST data will help investigate the frequency of quasars highly reddened by internal dust (cf. Sanders et al. 1989, Webster et al. 1995, Shaver et al. 1996; Malhotra, Rhoads, and Turner 1996). This should prove very interesting when the broad-band spectra of quasars are constructed from SDSS and 2MASS data. The FIRST quasars will also prove invaluable for understanding our selection effects; without it, we would not know of the existence of those quasars which lie directly in the stellar locus (cf., Figure 3.3.3). Faint stellar objects associated with ROSAT sources (Chapter 2.1 and Section 3.3.4g) are also very likely to be quasars, and will further increase the completeness of the quasar sample. Again, the completeness of the sample will be quantified with the Southern stripe survey of all stellar objects over an appreciable area of sky.
During the course of the Sloan Digital Sky Survey, spectra of approximately 100,000 quasars will be obtained with the SDSS spectrograph. The spectra, covering wavelengths from 3900 Å to 9200 Å at a resolution of 2000, will be of very high quality by current standards; at present only a few hundred quasar spectra exist with such resolution, signal-to-noise ratio, and wavelength coverage.
Figure 3.3.4 displays a simulated SDSS spectrum of a quasar with a redshift of 3.4 and g'=19.7 . These data should be typical of the lowest-quality quasar spectrum that will enter the SDSS data base. The upper two panels are the data from the blue side of the spectrograph; the lower two graphs are the red channel spectra. The data have been compressed for display purposes (each spectrograph channel in the figure has 1000 points, whereas the actual spectra will contain 2000 points per channel). It is clear that the spectra will contain a wealth of information about the properties of the quasar itself, as well as about the absorption lines due to material in the intergalactic medium.
The history of the study of the large scale spatial distribution of quasars has been almost entirely written in the past decade. The first large systematic investigation was performed by Osmer (1981); he found no significant clustering at z ~ 2 from a sample of 174 quasars found in a CTIO objective prism survey. Many subsequent programs, using relatively small sample sizes, also failed to detect any signs of quasar clustering (see Shaver 1988 for a review).

Simulated SDSS spectrum. The figure shows the blue channel of a z = 3.4, g' = 19.7 quasar. The spectrum has been rebinned so that there are only 1000 points per spectrum (the actual data will have 2000 points per spectrum).

Simulated SDSS spectrum. The figure shows the red channel of a z = 3.4, g' = 19.7 quasar. The spectrum has been rebinned so that there are only 1000 points per spectrum (the actual data will have 2000 points per spectrum). The effects of the dichroic filter, and the overlap region of the spectroscopic channels, have been suppressed in these figures.
This picture of randomly distributed quasars has changed in the past few years because of substantial increases in sample sizes, in particular the availability of large low-redshift samples (cf., Crampton 1992). The analysis by Shanks, Boyle, and Peterson (1988) of their sample of 423 quasars with z <= 2.2 produced strong evidence for the existence of quasar clustering on small (less than 10 h-1 Mpc) scales. Iovino and Shaver (1988) found a similar result for z < 1.5 quasars, but they could detect no significant clustering for quasars at redshifts above 1.5. A recent study by Andreani and Christiani (1992) combined the results from a number of surveys to produce a sample of ~ 1600 quasars; unlike Iovino & Shaver, their data was consistent with no change in the two-point correlation function as a function of redshifts for z <= 2.15 .
Crampton, Cowley, and Hartwick (1989) discovered what is to date the most convincing grouping of quasars; a total of 23 quasars with 1.0 < z < 1.2 located within a 2° field was identified from their CFHT survey. Another interesting set of probable physical pairs was discovered in a CCD/grism survey (Schneider, Schmidt, and Gunn 1994); among the 90 quasars with redshifts larger than 2.7 found in this program, there are three pairs of quasars that have an angular separation of less than 7 ' and have Delta z < 0.05 (cf., Kundic 1996). The strength of the quasar correlation function suggests that quasars are located in small groups of galaxies (Bahcall and Chokshi 1991).
At the present time the "conventional wisdom" (if this term can apply to such a rapidly changing subject) is that quasars are clustered on scales less than 10 h-1 Mpc for z < 2 ; at distances or redshifts larger than this the clustering disappears. It is clear that this subject would benefit enormously from the existence of a very large sample having well-defined selection properties. The SDSS will in this sense be ideal. The errors on the derived correlation function vary inversely with the sample size at small scales; therefore, we can expect an improvement in the sensitivity to clustering over existing samples by a factor of nearly 200! In the southern survey, we will probably perform a redshift survey of quasar candidates at least a magnitude fainter than that in the North (Section 5.5). This will not increase the volume covered in the survey but will explore less luminous objects with much larger space densities, and so will provide much better definition of the structure on intermediate scales.
On the theoretical front, Matsubara and Suto (1996) and Ballinger et al. (1996) have pointed out that a comparison of the radial and transverse dependence of the quasar correlation function in principle can yield a constraint on the cosmological constant. This measurement will not be easy; the effect is not large, and is mimicked to some extent by peculiar velocity effects. Nevertheless, the quasar sample will be big enough to attempt this measurement.
Quasars are in many respects our best probes of cosmic evolution because their enormous intrinsic luminosities (up to more than 1013Lsolar) allow them to be detected out to very large distances, and hence long look-back times. The first ten years of quasar research saw the largest known quasar redshift rise from 0.158 (Schmidt 1963) to 3.53 (Wampler, Robinson, and Baldwin 1973). This increase meant that one could study the most luminous objects and their environments at an era when the Universe was only about 10% of its current age; a startling gain in our grasp of the cosmos. The very existence of quasars at this epoch revealed valuable insights about the time scales for the formation of structure, and the discovery of the multitude of absorption features in the spectra of quasars, in particular the "Lyman alpha forest" (Lynds 1971), permitted investigation of non-luminous matter distributed throughout the Universe.
The search for high-redshift quasars is motivated by the fact that their existence places interesting constraints on quasar evolution and the early history of the Universe. If quasars are 107-109Msolar black holes accreting matter at the Eddington limit, then the e -folding time scale for the growth of the mass of the central object is ~4.4 x 108 years (Rees 1984 and references therein; Yi 1996). This is comparable to the age of the Universe at redshifts of 4-5 in currently fashionable cosmologies.

The spectrum of the most distant known quasar ( z = 4.90 ). This object was discovered using a four-filter/CCD survey. Note the strong absorption blueward of the Lyman alpha emission line (Schneider et al. 1991b).
Despite extensive efforts to locate ever more distant objects, the subsequent 13 years saw the largest known redshift increase only to 3.80 (Hazard, McMahon, and Sargent 1986). The last decade, however, has seen explosive growth in this field; these breakthroughs were made possible by improvements in detector technology and the rapid increase in the capabilities of computer hardware and software (Warren and Hewett 1990). The first redshift greater than 4 was found by Warren et al. (1987) in a multicolor survey that employed a filter scheme very similar to that being used for the Sloan Digital Sky Survey. The redshift record was broken at the rate of roughly once per year between 1987 and 1991; the most distant known object as of the time of this writing, also found in a multicolor survey, has a redshift of 4.90 (Schneider et al. 1991b).
Several surveys, using both multicolor and slitless spectra techniques, have been undertaken since 1991, but these programs have not discovered any quasars with redshifts larger than 4.9. It is becoming clear that quasars with redshifts of five or larger are exceedingly rare; in order to assemble a reasonable sized sample of such objects one must cover large areas of sky. This requirement is of course met by the SDSS; this survey should dramatically increase our understanding of the quasar luminosity function at high redshifts. Based on current results, we expect the SDSS to contain several thousand quasars with z > 3 and as many as 1000 with z > 4 . The SDSS data should permit identification of quasars at redshifts well above five, where Lyman alpha moves into the i' and z' bands. At present, it is a struggle to assemble a uniformly selected sample of 100 quasars with z > 3. As of this writing (December 1996), published studies have found about 50 quasars with z > 4 using a large range of search techniques.
With the new data, we can expect a resolution of the longstanding debate on the nature of the evolution of the quasar luminosity function and the question of whether the space density truly declines at redshifts larger than 3.5 (Osmer 1982). Figure 3.3.6 shows an estimate of the evolution of the spatial density of quasars with MB < -26 as a function of redshift produced by combining the results of the Hewett, Foltz, and Chaffee (1993) study (solid line for z < 2.5 ) with a recent high-redshift emission line survey (four points for z > 2.5 ; Schmidt, Schneider, and Gunn 1995). This picture of the evolution is qualitatively consistent with the results of Hewett et al. (1993), Warren et al. (1994), and Kennefick et al. (1995), although there are indications that the space density of the most luminous objects does not decline nearly as steeply with redshift as do the quasars used in the analysis that produced Figure 3.3.6 (Irwin, McMahon, and Hazard 1991). The luminosity function at redshifts larger than 4.5 remains quite uncertain, as only six such quasars are known.
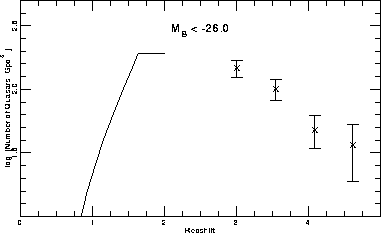
Quasar evolution. The solid line is the current best estimate of the evolution of the spatial density of luminous quasars with MB < -26 .
As discussed by Efstathiou and Rees (1988), the number of z ~ 5 quasars will place strong constraints on the cold dark matter model, where massive condensed structures would be expected to form at a later epoch. Turner (1991) describes the theoretical difficulties posed by the existence of the known z > 4 objects; Cavaliere and Padovani (1989) and Haehnelt and Rees (1993) discuss the constraints that the quasar luminosity function places on the intrinsic properties of quasars. The spectra of high-redshift quasars provide information about the production of metals in the early Universe (e.g., Hamann and Ferland 1992). The existence of even a few quasars with redshifts greater than 4.5 has stimulated theoretical investigations of the processes that could produce such rapid formation of massive objects (Loeb 1993; Loeb and Rasio 1994).
Since the discovery of individual quasars at redshifts larger than five would have important scientific implications, it is planned that a small number of fibers (3-5 per spectroscopic field) will be devoted to examination of faint objects (down to r' ~ 22 ) that are promising candidates for z > 5 quasars. Although the quality of these spectra will be rather low, the signature of a high-redshift quasar (strong Lyman alpha line combined with significant intergalactic absorption) is sufficiently unusual that a redshift determination will be possible.
The quasars found in the SDSS will also improve our understanding of the quasar luminosity function at lower redshifts. The best low-redshift ( z < 2 ) samples typically have a few hundred quasars, while the high-redshift studies typically contain but 100 objects. In practice it is difficult to tie these results together, because the techniques used to find the quasars often change as a function of redshift. The SDSS will produce a sample roughly two orders of magnitude greater in size than current programs, and will do so with a homogeneous selection system. The SDSS will certainly discover a large number of bright, low-redshift quasars; the CCD/grism survey of Schneider, Schmidt, and Gunn (1994) covered only 61 sq degrees and was designed to find z > 2.7 quasars, but still managed to discover three previously unknown quasars with z < 2 brighter than r = 16.7.
The number of bright, high-redshift quasars will be greatly enlarged as a result of this survey. Over 11,000 quasars with B < 18 should be discovered based on the numbers in Table 3.3.1; of these, approximately 10% will have z > 2.5 . Thus, there should be a sample of more than a thousand bright, high redshift objects available for study with 8-m class telescopes, which will have enough light gathering power to permit the use of spectral resolutions as high as 60,000. At these resolutions, the intergalactic medium at high redshift can be studied in unprecedented detail via the absorption lines. (A good example of state-of-the art measurements is the R =36,000 spectrum at a signal-to-noise ratio of 160 of QSO1422+231 by Songaila and Cowie 1996). We will be able to obtain valuable new information on the nature and evolutionary history of the intergalactic medium at large redshifts and on the properties of galaxies that intersect the line of sight but are otherwise too distant and too dim to be seen.
The survey will be ideal for investigating the associations between low redshift quasars and galaxies. Ellingson, Yee, and Green (1991), using a sample of 63 nearby ( 0.3 < z < 0.6 ) quasars, show that while radio-quiet quasars are rarely found in rich clusters, radio-loud quasars frequently reside in Abell richness class 1 or richer clusters. The distinction between the clustering properties of radio-quiet and radio-loud quasars has recently been questioned (Fisher et al. 1996) in work that shows that the quasar-galaxy correlations are very strong. Since the SDSS will provide deep imaging of all of the quasar fields, it will be possible to study the relationship between quasars and their local environments for a very large number of quasars, especially in the Southern stripe. This line of investigation will undoubtedly yield important information about the relation between galaxy environments, interactions, and the phenomenon of active nuclei for many more than the ~ 50 cases studied so far.
Perhaps the greatest scientific contribution to date arising from quasar research comes not from what their properties reveal about galaxy formation or physical processes under extreme conditions, but their use as "cosmic flashlights" to expose the presence of non-luminous matter. When quasars were discovered whose redshifts were sufficiently large to bring the Lyman alpha transition into the optical band ( z > 2 ; Schmidt 1965), it was quickly realized that studies of the absorption lines in the spectra of these distant beacons might yield valuable insights into the properties of "dark matter" (Gunn and Peterson 1965; Bahcall and Salpeter 1965). The subsequent 30 years have more than fulfilled the early expectations; studies of quasar absorption lines systems have provided vast amounts of information about the physical conditions of the intergalactic medium and the distribution of galaxies. Until recently, the investigation of quasar absorption lines was, to a large extent, confined to intermediate or high redshifts (the strong resonance lines of the cosmically abundant light elements all occur in the ultraviolet), but the past few years observations with the ultraviolet spectrographs of HST have permitted investigation of the local intergalactic medium (Bahcall et al. 1993, 1996). Recent reviews of quasar absorption lines are presented by York (1994) and Meylan (1995).
The impact of general intergalactic absorption on the spectra of quasars is vividly demonstrated in Figure 3.3.7. This graph displays the depression (fraction of light absorbed) in quasar spectra at wavelengths blueward of the Lyman alpha emission line. We ignore the complete absorption which occurs when a strong Lyman limit system is detected. The amount of absorption rises from zero for low redshift quasars (observed with the International Ultraviolet Explorer) to over 50% at redshifts larger than four. Figure 3.3.5, the spectrum of a z = 4.90 quasar, shows how pronounced the absorption becomes at high redshift.
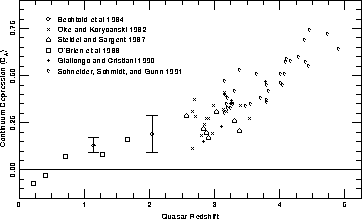
Absorption by intergalactic gas as a function of redshift. At redshifts larger than four, more than half of the light is absorbed (Schneider et al. 1991a).
Quasar absorption lines are seen from three types of systems: 1) systems with only the Lyman series lines of H I detected (often only Lyman alpha is seen), with a wide and not strongly clustered distribution in redshift space; 2) systems with lines of high and/or low ionization states of heavy elements; and 3) broad absorption line (BAL) systems.
Systems of type 1 make up the "Lyman alpha forest" (Lynds 1971). Heavy element lines are not generally seen for H I column densities below 1015 cm-2 , either because the systems are primordial (Sargent et al. 1980) or because the abundances are too low to yield detectable absorption features with the instrumentation used. Recent evidence is conflicting on the relationship of these systems to galaxies. They may be directly associated with galaxies (Lanzetta et al. 1995), loosely associated with galaxies (York et al. 1986, Bowen et al. 1996), or not associated with galaxies (Shull et al. 1996, see also arguments in Bowen et al. 1996).
Systems of type 2 generally form a continuum with type 1 systems, in terms of strength of heavy element lines; the latter are weak but detectable as the column densities increase from 1015 to 1017 cm-2 (Meyer and York 1987, Tytler and Fan 1994, Songaila and Cowie 1996). At higher column densities, the Lyman limit of H I is detectable at rest frame 912 Å (Tytler 1981; see the region 5180 to 5280 Å in Figure 3.3.5). Above 1020 cm-2 , the Lyman alpha and a few other lines of the Lyman series develop damping wings that are discernible even in the heavily blended forest of weaker lines. Abundances of the heavy elements, such as O, Si, Fe, Zn and Cr are uncertain for many observational reasons, but all indications are that at high z, the abundances are very low (0.1 to 1% of Solar), rising to just about 10% of Solar at z < 1 (Timmes et al. 1995). When systems of type 2 are within a few thousand kilometers per second of the redshift of the background QSO, they are referred to as "associated "and may provide a sample of gas processed by and ejected from the QSO.
Systems of type 3 contain deep absorption troughs on the short wavelength side of the main QSO emission lines, with velocity widths of up to 10,000 km s -1 . There is some weak evidence that they may be related to the narrower associated systems (Jannuzi et al. 1996). As many as 10% of QSOs show the BAL phenomenon (Weymann et al. 1991); see Section h below.
The Lyman alpha forest (type 1 lines) makes up the general depression that increases in redshift as noted above (Figure 3.3.7). The number of these lines increases with redshift as (1+z)2.3 past z=2 (Murdoch et al. 1986, Lu et al. 1991), whereas the number of heavy element line systems per unit z decreases above z=2 (Steidel 1990). The latter effect may be largely related to the decrease of the abundance of heavy elements with increasing redshift. The Lyman alpha forest has more lines at low z than expected from the above law (Bahcall et al. 1993), whereas too little is yet known about the heavy element line systems at z<1 to make a general statement.
The origin of the type 2 systems is still controversial. Some may be associated with galaxian disks (Wolfe et al. 1986), some may be associated with star forming building blocks of modern galaxies (Yanny and York 1992, Pascarelle et al. 1996) and some may be loosely associated with the outer parts of modern galaxies (Churchill et al. 1996). Whatever the origin, the Lyman limit absorption from these systems accounts for the removal of large amounts of radiation shortward of the wavelength that corresponds to (1+z)x 912 Å . Since the system redshifts are generally uncorrelated from one quasar to the next on large scales, the absorption from the limits introduces scatter in the QSO tracks of Figure 3.3.1. These same Lyman limit systems offer a direct probe of neutral hydrogen in the Universe at early times (Meiksin and Madau 1993) and provide the mean free path of ionizing radiation at these epochs.
The SDSS quasar spectra will be well suited, in wavelength coverage, spectral resolution, and signal-to-noise ratio, for many absorption line studies (although it certainly will not compete with the very high-resolution studies of absorption lines carried out, e.g., with the HIRES instrument on the Keck telescope; cf., Songaila and Cowie 1996 for an example of the spectra that are attainable). The Lyman alpha , C IV, and Mg II lines will be visible at redshifts 2.3-6.4, 1.6-4.8, and 0.5-2.2, respectively, and the Lyman-limit can be seen at redshifts greater than 3.4. A one hour exposure on a g' = 19.7 object with the SDSS spectrograph will produce a spectrum with a signal-to-noise ratio (per 2.5 Å resolution element) of 14 at 5500 Å. The spectra will have a 5 sigma limit on the observed equivalent widths of unresolved absorption lines of ~0.9 Å, corresponding to rest frame equivalent widths a factor of (1 + z) smaller, and comparable to the limits of various surveys of absorption lines extant in the literature. At high redshifts, the SDSS spectra will not have sufficient resolving power to separate the individual lines in the Lyman alpha forest, but the properties of the Lyman alpha lines can still be investigated in some detail using statistical techniques developed in the past few years for quasar absorption line studies (Jenkins and Ostriker 1991; Webb et al. 1992; Press, Rybicki, and Schneider 1993). The largest published absorption line surveys (e.g., Steidel and Sargent 1992) contain at most ~ 100 quasars each having data for less than an octave of wavelength coverage. This survey will contain uniform data for 100,000 objects with more than an octave of coverage. If one adds up the redshift range that will be covered for all of our quasars, we find Delta z = 80,000 for 0.5 < z < 1.5 , Delta z = 60,000 for 1.5 < z < 2.5 , and Delta z ~ 4,000 for 2.5 < z < 3.5 .
Current absorption line studies show that one can expect to see about one galaxian absorption system per unit redshift per quasar. The lines in which these can be detected include C IV, lambdar~= 1550 Å; Si IV, 1393, 1402 Å; Si II, 1526 Å; Al II, 1670 Å; Fe II, five lines in the range 2300-2600 Å; Mg II, 2795, 2802 Å; and Mg I, 2852 Å. At the equivalent width limits of our faintest quasars, two-thirds of absorption-line systems in the literature have only C IV lines at lambda > 4000 Å; this doublet is easily recognizable with the 2.5 Å SDSS spectral resolution. The SDSS spectra should result in the detection of 0.5 absorption systems per unit redshift that contain either multiple species or only C IV lines. The number of galaxian absorbers per unit redshift increases from z = 0 to z = 2 to 2.5, then decreases. Thus the number of absorbers found in the survey will be 40,000 ( 0.5 < z < 1.5 ), 30,000 ( 1.5 < z < 2.5 ), and approximately 2,500 for 2.5 < z < 3.5 . The detected objects have typical separations of tens of Mpc, similar to the separation of the survey quasars.
Key information on galaxies and large-scale structure at large redshifts can be obtained simultaneously with the galaxy and quasar surveys described above. Even though the luminosity of stars in distant galaxies may not be discernible, those galaxies will produce gas absorption lines in spectra of objects behind them. Aggregates containing but 10-6 of a galaxy mass can be detected in this way. Steidel et al. (1994) have shown that follow-up of such systems on larger telescopes is an ideal way to identify galaxy populations at high redshifts for evolution studies.
The sample of galxian absorbers provides about 1000 objects in each of several volumes the size of the extremely well sampled nearby galaxy surveys, allowing clustering to be measured on very large scales (Quashnock et al. 1996; cf., the discussion in Section 3.1.4.4). The sample size is so large that the correlation function on scales of 50 to 100 Mpc can be determined in each volume to higher precision than we now know the correlation function within the local volume to 100 Mpc, and can be determined separately for fifty volumes of 1 Gpc 3. The evolution of the correlation function on large scales is of great interest in distinguishing low density and high density universes.
The large samples will include an appreciable subset of strong line systems ( ~ 10%) with detectable lines of many elements (those given above plus chromium, nickel, cobalt, copper and zinc). This sample will be adequate, when studied with larger telescopes, to distinguish directly the gradual build-up of grains and of the heavy element pool in galaxies from z = 4 to the present (Pettini et al. 1994, Lu et al. 1996, Lauroesch et al. 1996).
Since the sample is so large, one can break the data into subsamples of significant size, selected only by direction. The statistics of the subsamples can be analyzed in a variety of ways (number of absorbers per unit redshift; coarse abundances; cosmic radiation pumping of atomic levels; galactic radiation fields from ionization states of observed species; and changes of these quantities with time) to address the question of the homogeneity and isotropy of the universe on the largest scales yet achieved.
Finally, the survey will greatly enhance the ability to study coherent structure of the intergalactic gas by the inevitable discoveries of pairs (or sets) of quasars with separations of only a few arcminutes (e.g., Jakobsen et al. 1986; Fang et al. 1996); this subject is discussed in detail in Section 3.1.4.4.
A large data base on the emission line and continuum properties of quasars will be produced by the survey. Figure 3.3.4 displays a simulated spectrum of a quasar with a redshift of 3.4 and an apparent brightness of g' ~ 19.7 , our survey limit. Since the quality of all of the quasar spectra obtained in the survey will be at least this high, it is obvious that the set of 100,000 spectra will allow a number of detailed investigations of the intrinsic properties of quasars.
We know that quasar spectra differ significantly in their line widths and strengths, but no obvious pattern has emerged except for the "Baldwin Effect": lower luminosity quasars tend to have stronger emission lines (Baldwin 1977). However, emission line data and photometry of quasars are very important for testing physical models of quasars, and the new data will be by far the best available for such work. The best continua/emission line studies to date contain of the order of 100 quasars; the analyses presented in Steidel and Sargent (1991) and Tytler and Fan (1992) are examples of the scientific questions that can be addressed using a set of high-quality quasar spectra.
Few topics in astronomy have captured the popular (and professional, for that matter) imagination as vividly as gravitational lenses. The fact that standard theories reproduce the basic observational parameters of several lenses (e.g. Q 0957+561, the original "double quasar"; cf., Grogin and Narayan (1996), 2016+112, and 2237+0305) indicates that the general theory of relativity applies on scales of the sizes of galaxies. It also confirms our basic understanding of cosmological distances and redshifts as well as galaxy mass distributions. Measurements of time delays between images (Kundic et al. 1996, and references therein) and possible microlensing events (Irwin et al. 1989) are among the most exciting observational results of the past few years. In addition, the observed frequency of lensing has been used to place constraints on the masses of galaxies and of the value of the cosmological constant (Turner, Ostriker, and Gott 1984; Fukugita and Turner 1991; Maoz and Rix 1993).
The known cases of lensing have frequently been serendipitous discoveries, though lens surveys at optical wavelengths (Surdej et al. 1987; Yee, Filippenko, and Tang 1993) and radio (Lawrence et al. 1984) wavelengths have experienced some success. In particular, the Hubble Space Telescope Survey for gravitational lenses (Bahcall et al. 1992; Maoz et al. 1993) examined Planetary Camera images of 498 quasars, and discovered the most distant known lens (Q 1208+1011 at a redshift of 3.80 (Maoz et al. 1992). Most of the known lenses have component separations of several arcseconds; in some of these cases a fairly rich cluster of galaxies contributes appreciably to the lensing mass (although there are a number of controversial "dark" lenses). It has long been predicted (Turner, Ostriker, and Gott 1984) that there should be many cases of image separations of about one arcsecond (arising from lensing by a single galaxy). The calculation of the expected frequency involves rather few assumptions, and one expects of order 10 -3 of all quasars in the magnitude range 18-21 to have double images with separations of this order (Ostriker and Vietri 1986); in 60% of these cases the images differ in brightness by less than one magnitude. The Palomar Sky Survey lacks the angular resolution required to distinguish these objects.
The SDSS should have an enormous impact on this field because of its large areal coverage, its high angular resolution, and the large dynamic range of its detectors. We expect there to be ~ 100 lenses in the spectroscopic survey, and about 1000 in the fainter quasar candidate list (objects with colors of quasars but too faint to be included in the spectroscopic survey). In the latter case, the fraction of candidates that are lenses should be extremely high; obviously two closely-spaced faint stellar objects with similar quasar-like colors are even more likely to be a lensed quasar than any single object with quasar-like colors is to be a single quasar. These predicted numbers are likely to be overestimates because of dust extinction in the lensing galaxies, but the larger lensing cross-sections of early-type, big-bulge systems with little or no dust makes this less important than one might think. In any case, many of the most promising potential uses of gravitational lenses as cosmological probes depend on the analysis of a substantial and statistically well controlled sample of lens systems which the SDSS will produce. We will not be able to do spectroscopic follow-up on most of our lens candidates, of course, because of our fiber size and finite minimum fiber separation, but the sample will not be so large as to preclude follow-up on other telescopes, and we do not expect any dearth of outside interest in this follow-up.
More than a quarter century has elapsed since the discovery of X-ray emission from the first quasi-stellar object, 3C273 (Bowyer et al. 1970). Since that time, observational progress has been steady. We now have integrated X-ray flux measurements for several hundred QSOs, both from targeted observations of objects selected from pre-existing catalogs, and from post facto optical identifications of serendipitously detected X-ray sources. What have we learned?
At the highest level, it is clear that studies of QSOs at X-ray wavelengths are essential. Although there are considerable variations from object to object, in general as much flux is dissipated in soft X-rays as in the visible part of the spectrum (i.e., f(0.5-5 keV)/f(opt)~1 ), and most of the total, bolometric energy dissipation of a typical QSO emerges as ionizing radiation ( f(E>1 keV)/f(E<1 keV)>1 ). Furthermore, the X-ray flux is often found to be strongly variable on a timescale of hours, appreciably faster than variations seen in other regions of the spectrum, presumably implying an origin within tens of A.U. of the center of the system. As this is comparable to the Schwarzschild radius of a 109Msolar black hole, it seems apparent that X-ray observations probably take us as deep into the central emission region of a QSO as is possible to probe.
It is interesting to consider the impact of X-ray observations on our understanding of the physics of QSOs. As the optical and radio properties of QSOs vary widely from object to object, and in X-rays only accurate broadband flux data, rather than dispersive spectroscopy, are available, workers thus far have studied ensemble X-ray characteristics of samples of objects as a function of their optical or radio characteristics. (We note in passing that this approach may change radically within a few years with the launch of AXAF, XMM, and ASTRO-E, when high-resolution X-ray spectroscopy at X-ray flux levels appropriate for dozens of QSOs will finally become routinely available.) Such X-ray studies have provided a variety of tantalizing facts, but limited global advances in our understanding of QSOs. For example, we understand that Lx/Lopt is dependent on Lopt (Tananbaum et al. 1979), and that radio-loud QSOs have systematically different X-ray spectra and luminosity than radio-quiet objects (Avni and Tananbaum 1986; Schartel et al. 1996a, 1996b). Furthermore, most workers now agree that the soft component of the diffuse X-ray background radiation is due in the majority to emission from a superposition of distant point sources, chiefly QSOs and related active galactic nuclei, although there are still significant uncertainties remaining (Fabian and Barcons 1992). In addition, it is clear that Broad Absorption Line QSOs are not detectable X-ray sources (Green and Mathur 1996), and that (broadband) QSO X-ray spectra become complex and diverse at E< 1 keV, almost surely indicating multi-component emission processes and/or reflection/reprocessing of emission from multiple sites (Laor et al. 1994, Fiore et al. 1995). While all of these are wonderful achievements indeed, and have brought the field of X-ray observations of QSOs to a vastly more sophisticated state than the first few 3 sigma flux detections of 25 years ago, it is probably a fair statement that X-ray observations have not yet yielded fundamental new insights into such areas as QSO energy sources or evolution.
Where are the prospects for future progress in this field? As noted above, the era of routine X-ray spectroscopy at lambda / Delta lambda ~103, finally comparable to optical resolution, can be expected shortly, and will surely provide a huge jump forward. We point out here that the availability on the same timescale of the very large ( 105 object) SDSS QSO sample, with its perfectly homogeneous and high signal to noise ratio optical spectroscopy, will also be a new and vital tool in the study of the X-ray properties of QSOs. Indeed, because at the conclusion of the SDSS, ~90% of all known QSOs will be SDSS QSOs, it will be virtually impossible to avoid the issue of interaction between extragalactic X-ray astronomy and the SDSS. The "typical" SDSS QSO, with 18<r'<19 , will have -13 < logfx < -12 erg cm -2 s -1 in the (0.5-5.0) keV band (Stocke et al. 1991), and is thus very well matched to the capabilities of current X-ray imaging surveys such as ROSAT, and future spectroscopic instruments on AXAF, XMM, and ASTRO-E.
The consequences of this match are multiple, but here we consider as examples two specific issues, ROSAT All Sky Survey (RASS) QSOs, and AXAF/XMM/ASTRO-E X-ray spectroscopic targets. As we noted in Chapter 2.1, the amalgam of the RASS data with SDSS will yield broadband X-ray fluxes for ~104 SDSS QSOs, each with a high signal-to-noise ratio optical spectrum obtained with the identical equipment and observing protocol. A smaller but still significant number (i.e., orders of magnitude larger than ever before) will also have X-ray spectral data or at least hardness ratios. For the first time, we will have hundreds of QSOs in each redshift or luminosity bin, each with accurate, homogeneous X-ray and optical fluxes, to understand issues of luminosity dependences and evolution. For the first time, we will have a huge, homogeneous set of optical emission line fluxes to compare with QSO X-ray fluxes, a potent arsenal to finally unravel such issues as the elusive "Baldwin effect," a striking but poorly understood correlation of ionizing radiation luminosity with emission line strength (e.g., Green 1996). As AXAF, XMM, and ASTRO-E open the era of QSO X-ray line spectra, the SDSS QSO spectroscopic bank will be a mandatory interpretive tool. We will wish to compare X-ray lines from multiply ionized heavy elements with optical lines of lower excitation; SDSS will provide an "on demand" and beautifully homogeneous data archive of the necessary optical spectroscopic data. X-ray edges and spectral slopes will demand knowledge not just of local galactic NH for interpretation, but also of the presence, redshift, and opacity of intervening intergalactic absorbers, e.g., the Ly alpha forest, damped Ly alpha, and Ly-limit systems; again, SDSS provides these data immediately and uniformly for huge numbers of potential targets.
BL Lacertae objects are a subclass of active galaxy characterized by nonthermal continua with strong radio and X-ray emission, nearly featureless optical spectra, high polarization, and marked intensity variability at all wavelengths (Kollgaard 1994, Urry and Padovani 1995). Most models for the BL Lac phenomena invoke a relativistic beam viewed nearly along the line of sight (Blandford and Rees 1978), but others (for example) invoke gravitational microlensing of background quasars viewed through foreground galaxies (Ostriker and Vietri 1990).
Because of their rarity (only ~ 2% of the objects in current QSO/AGN catalogs are BL Lacs) and unusual properties, large and well-defined samples of BL Lacs are eagerly sought, but until very recently have proven extraordinarily difficult to assemble. Their rarity demands large areal sky coverage, and yet their unusual spectral energy distributions and lack of strong spectral features render past QSO/AGN optical-selection (e.g., UV-excess or objective prism surveys) woefully incomplete for BL Lacs. Despite numerous attempts, there are currently only a very small number of homogeneous BL Lac samples of even modest size, and these few have been assembled via exploitation of strong radio or X-ray emission. These few samples have nonetheless produced some fascinating results. For example, the X-ray-selected sample of the Einstein Extended Medium Sensitivity Survey (Morris et al. 1991) has provided an initial estimate of the luminosity function for BL Lacs that suggests "negative" evolution; that is, in marked contrast to quasars, BL Lac objects appear to be less common or less luminous in the past. However, even this tantalizing result relies on only a few dozen objects.
Many recent efforts to obtain well-defined BL Lac samples utilize a combination of multiwavelength information from the optical, X-ray, and radio bands to obtain high selection efficiency. Stocke et al. (1991), Perlman et al. (1996), and other groups exploit the fact that BL Lacs occupy distinctive region(s) in flux-ratio plots constructed from such multiwavelength information; e.g., BL Lacs fall in distinctive regions of fr/fopt vs. fx/fopt plots compared with other object classes. (But note there may be some added complexity in that X-ray- and radio-selected BL Lacs may favor somewhat different regions of such plots, e.g. Brinkmann et al. 1996). The combination of SDSS optical flux information (in 5 colors) over pi ster of sky, coupled with X-ray information from the RASS, and perhaps radio information from FIRST and other radio surveys, will surely provide an excellent opportunity for selection of a large homogeneous BL Lac sample. In fact, the efficacy of utilizing RASS data for very large area combined X-ray/optical/radio BL Lac selection -- or even just optical/X-ray selection -- has already been demonstrated (e.g., Kock et al. 1996, Nass et al. 1996). For example, Nass et al. (1996) selected 34 BL Lacs in 6000 deg² of sky jointly covered by the RASS and the Hamburg QSO (optical) survey (Wisotzki et al. 1996); candidate objects were selected initially from their high ratios of fx/fopt , characteristic of BL Lacs, and then followed up with optical spectra. These authors estimate that an additional ~200 BL Lacs await discovery even in this same 6000 deg² of sky to a modest X-ray flux limit of ~ 10-12 erg cm -2 s -1 . Thus in the SDSS survey region of pi ster, it is expected that available combinations of optical, X-ray, and perhaps radio flux information will aid in the homogeneous selection of a BL Lac sample comprised of several hundreds of objects (compared to the handful of extant homogeneous samples, which contain ~ 20-60 objects each).
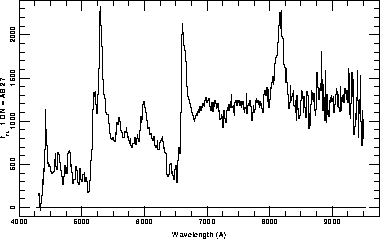
The spectrum of BAL quasar PC 2330+0125 ( z = 3.28). The three strongest emission lines, in order of increasing wavelength, are Lyman alpha , C IV, and C III. Note the deep, broad, blueshifted absorption troughs due to Lyman alpha and C IV.
It is worth noting that flux sensitivities reached in SDSS, RASS, and even FIRST are mutually well-matched for a large-area multiwavelength sky survey for BL Lacs. For example, a BL Lac with an X-ray flux of a few times 10-12 erg cm -2 s -1 might be expected to have an optical magnitude ~ 20 , and a radio flux of a few mJy. For many of these BL Lacs, SDSS will not only provide optical flux measures in 5 colors, but also at least initial confirming optical spectra as well. For example, RASS X-ray sources also detected in radio catalogs will be amongst those X-ray sources targeted with highest priority for SDSS optical spectra, and many other FIRST radio sources are also intended for SDSS spectroscopy, independent of whether or not they are X-ray sources.
The spectrum of the strong-lined, z = 3.68 quasar PC 1033+4750. The two prominent emission lines are Lyman alpha and C IV.
With the large size of the quasar sample will come the opportunity to study relatively rare objects. For example, quasars with Broad Absorption Lines (BALs) are ejecting matter at speeds of 10% the speed of light or more. The spectrum of a typical BAL quasar is shown in Figure 3.3.8. Establishing what fraction of quasars exhibit the BAL phenomenon and studying their spectra will reveal information on processes occurring very close to the central engine, in particular the geometry of the quasar emission mechanism, the production of metals in the early Universe, and the physics of outflows.
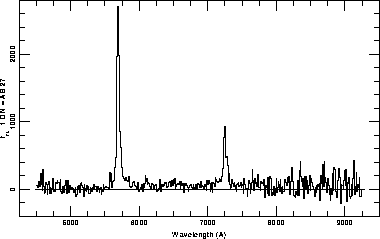
The sample will also reveal other rare objects which at present are mostly curiosities, but which could contain clues to the evolution of abundances in quasars and their relation to more normal galaxies at high redshift. For example, will some primeval galaxies with emission lines be found in the quasar survey? How will they compare with quasars? An example of an exotic object found in a CCD quasar survey (Schneider, Schmidt, and Gunn 1994) is displayed in Figure 3.3.9. The spectrum of this z = 3.68 quasar is dominated by strong, relatively narrow emission lines; the observed equivalent width of the Lyman alpha line is more than 1500 Å. The SDSS quasar data base should contain hundreds of quasars with characteristics that have rarely, if ever, been detected with current programs.
The SDSS will bring quasar samples up to the size of current galaxy surveys from which the first indications of large scale structure and voids were detected. We may expect similarly important discoveries to arise, now at much higher redshift. In addition, the quasar sample will yield a wealth of information on the intrinsic properties of quasars, the evolution of the luminosity function of quasars with time, and the dark intergalactic medium. It is clear that the quasar "spinoff" produced by SDSS represents a great advance over present efforts, and will almost certainly influence our picture of the large scale structure of quasars as significantly as the Shane-Wirtanen catalog did for galaxies.
Andreani, P., and Cristiani, S. 1992, ApJL 398, 13.
Avni, Y., and Tananbaum, H. 1986, ApJ 305, 83.
Bahcall, J.N., Bergeron, J., Boksenberg, A., Hartig, G.F., Jannuzi, B.T., Kirhakos, S., Sargent, W.L.W., Savage, B.D., Schneider, D.P., Turnshek, D.A., Weymann, R.J., and Wolfe, A.M. 1993, ApJSuppl 87, 1.
Bahcall, J.N., Bergeron, J., Boksenberg, A., Hartig, G.F., Jannuzi, B.T., Kirhakos, S., Sargent, W.L.W., Savage, B.D., Schneider, D.P., Turnshek, D.A., Weymann, R.J., and Wolfe, A.M. 1996, ApJ 457, 19.
Bahcall, J. N., Maoz, D., Doxsey, R., Schneider, D., Bahcall, N., Lahav, O., and Yanny, B. 1992, ApJ 387, 56.
Bahcall, J.N., and Salpeter, E.E. 1965, ApJ 142, 1677.
Bahcall, J.N., and Soneira, R.M. 1981, ApJSuppl 47, 357.
Bahcall, N.A., and Chokshi, A. 1991, ApJL 380, 9.
Baldwin, J.A. 1977, ApJ 214, 679.
Ballinger, W.E., Peacock, J.A., and Heavens, A.F. 1996, preprint (astro-ph/9605017).
Becker, R.H., White, R.L., and Helfand, D.J. 1995, ApJ 450, 559.
Blandford, R. D., and Rees, M. J. 1978, in Pittsburgh Conference on BL Lac Objects, ed. A. N. Wolfe (Pittsburgh U.: Pittsburgh), 328.
Bowen, D. B., Blades, J. C., and Pettini, M. 1996, ApJ 464, 141.
Bowyer, C. S., Lampton, M., Mack, J., and deMendonca, F. 1970, ApJLett 161, 1.
Boyle, B.J., Shanks, T., and Peterson, B.A. 1988, MNRAS 235, 935.
Brinkmann, W., Siebert, J., Kollgaard, R. I., and Thomas, H-C. 1996, AstrAp 313, 356.
Cavaliere, A., and Padovani, P. ApJL 340, 5.
Christiani, S. et al. 1995, A&AS, 112, 347.
Churchill, C.W., Steidel, C. C. and Vogt, S. S. 1996, ApJ 471, 164.
Crampton, D.C. 1992, The Space Distribution of Quasars, ASP Conf. Series 21.
Crampton, D.C., Cowley, A.P., and Hartwick, F.D.A. 1987, ApJ 314, 129.
Crampton, D.C., Cowley, A.P., and Hartwick, F.D.A. 1989, ApJ 345, 59.
Efstathiou, G., and Rees, M.J. 1988, MNRAS 230, 5p.
Ellingson, E., Yee, H.K.C., and Green, R.F. 1991, ApJ 371, 49.
Fabian, A. C., and Barcons, X. 1992, AnnRevAAp 30, 429.
Fang, Y., Duncan, R. C., Crotts, A., and Bechtold, J. 1996, ApJ 462, 77.
Fiore, F., Elvis, M., Siemiginowska, A., Wilkes, B. J., McDowell, J. C., and Mathur, S. 1995, ApJ 449, 74.
Fisher, K.B., Bahcall, J.N., Kirhakos, S., and Schneider, D.P. 1996, ApJ 468, 469.
Francis, P.J. 1996, P.A.S.A. 13, 212.
Fukugita, M., and Turner, E.L. 1991, MNRAS 253, 99.
Green, P. J. 1996, ApJ 467, 61.
Green, P. J., and Mathur, S. 1996, ApJ 462, 637.
Green, R.F., Schmidt, M., and Liebert, J. 1986, ApJSuppl 61, 305.
Greenstein, J.L., and Liebert, J. 1990, ApJ 330, 662.
Grogin, N.A., and Narayan, R. 1996, ApJ 464, 92.
Gunn, J.E., and Peterson, B.E. 1965, ApJ 142, 1633.
Gunn, J.E., and Stryker, L.L. 1983, ApJSuppl 52, 121.
Haehnelt, M.G., and Rees, M.J., 1993, MNRAS 263, 168.
Hall, P.B., Osmer, P.S., Green, R.F., Porter, A.C., and Warren, S.J. 1996a, ApJ 471, 1073.
Hall, P.B., Osmer, P.S., Green, R.F., Porter, A.C., and Warren, S.J. 1996b, ApJSuppl 104, 185.
Hamann, F., and Ferland, G.J. 1992, ApJL 391, 53.
Hartwick, F.D.A, and Schade, D. 1990, AnnRevAAp 28, 437.
Hazard, C., McMahon, R.G., and Sargent, W.L.W. 1986, Nature 322, 38.
Hewett, P.C., Foltz, C.B., and Chaffee, F.H. 1993, ApJL 406, 43.
Hewett, P.C., Foltz, C.B., and Chaffee, F.H. 1995, AJ 109, 1498.
Iovino, A., and Shaver, P.A., 1988, in Large Scale Structure of the Universe, IAU Symposium 130, J. Audouze et al. eds., p. 572.
Irwin, M.J., McMahon, R.G., and Hazard, C. 1991, in The Space Distribution of Quasars, ASP Conf. Series 21, D.C. Crampton, ed. (Brigham Young University: Provo), p. 117.
Irwin, M.J., Webster, R.L., Hewett, P.C., Corrigan, R.T., and Jedrzejewski, R.I. 1989, AJ 98, 1989.
Jakobsen, P., Perryman, M.A.C., Ulrich, M.H., Machetto, F., and Di Serego Alighieri, S. 1986, ApJLett 303, 27.
Jannuzi, T. T., Hartig, G. F., Kirhakos, S., Sargent, W. L. W., Turnshek, D. A., Weymann, R. J., Bahcall, J. N., Bergeron, J., Boksenberg, A., Savage, B. D., Schneider, D. P. and Wolfe, A. M. 1996, ApJL 470, 11.
Jenkins, E.B., and Ostriker, J.P. 1991, ApJ 376, 33.
Kennefick, J.D., Djorgovski, S.G., and de Carvalho, R.R. 1995, AJ 110, 2553.
Kennefick, J.D., Djorgovski, S.G., and de Carvalho, R.R. 1996, AJ 111, 1816.
Kock, A., Meisenheimer, K., Brinkmann, W., Neumann, M., and Siebert, J. 1996, AstrAp 307, 745.
Kollgaard, R. I. 1994, Vistas in Astronomy, 38, 29.
Koo, D.C, and Kron, R.G. 1988, ApJ 325, 92.
Kundic, T. 1996, PhD. Thesis, Princeton University.
Kundic, T. et al. 1996, preprint (astro-ph/9610162).
La Franca, F., and Christiani, S. 1996, preprint (astro-ph/9612181).
Lanzetta, K. M., Bowen, D. V., Tytler, D. and Webb, J. K. 1995, ApJ 442, 538.
Laor, A., Fiore, F., Elvis, M., Wilkes, B. J., and McDowell, J. C. 1994, ApJ 435, 611.
Lauroesch, J. T., Truran, J. W., Welty, D. E., York, D. G. 1996, PASP 108, 641.
Lawrence, C.R., Schneider, D.P., Schmidt, M., Bennett, C.L., Hewitt, J.N., Burke, B.F., Turner, E.L., and Gunn, J.E. 1984, Science 223, 46.
Liebert, J., Dahn, C.C., and Monet, D.G. 1988, ApJ 332, 891.
Loeb, A. 1993, ApJ 403, 542.
Loeb, A., and Rasio, F.A. 1994, ApJ 432, 52.
Lu, L., Sargent, W. L. W., Barlow, T. A., Churchill, C.W., and Vogt, S.S. 1996, ApJSuppl 107, 475.
Lu, L., Wolfe, A.M., and Turnshek, D.A. 1991, ApJ 367, 19.
Lynds, C.R. 1971, ApJLett 164, 73.
Malhotra, S., Rhoads, J., and Turner, E.L. 1996, M. N. R. A. S., submitted (astro-ph/9610233).
Maoz, D., Bahcall, J.N., Schneider, D.P., Bahcall, N.A., Djorgovski, S., Doxsey, R., Gould, A., Kirhakos, S., Meylan, G., and Yanny, B. 1993, ApJ 409, 28.
Maoz, D., Bahcall, J.N., Schneider, D.P., Doxsey, R., Bahcall, N.A., Filippenko, A.V., Goss, W.M., Lahav, O., and Yanny, B. 1992, ApJL 386, 1.
Maoz, D., and Rix, H.-W. 1993, ApJ 412, 34.
Matsubara, T., and Suto, Y. 1996, ApJL 470, 1.
Meiksin, A. and Madau, P. 1993, ApJ 412, 34.
Meyer, D. M. and York, D. G. 1987, ApJL 319, 45.
Meylan, G. 1995, QSO Absorption Lines, (Springer-Verlag: Berlin).
Moller, P., and Jakobsen, P. 1990, AstrAp 228, 299.
Morris, S. L., Stocke, J. T., Gioia, I. M., Schild, R., Wolter, A., Maccacaro, T., and Della Ceca, R. 1991, ApJ 380, 49.
Murdoch, H.S., Hunstead, R.W., Pettini, M., and Blades, J.C. 1986, ApJ 309, 19.
Nass, P., Bade, N., Kollgaard, R. I., Laurent-Muehleisen, S. A., Reimers, D., and Voges, W. 1996, AstrAp 309, 419.
Ng, Y.K. 1994, PhD. Thesis, Leiden University, The Netherlands.
Osmer, P.S. 1981, ApJ 247, 762.
Osmer, P.S. 1982, ApJ 253, 28.
Ostriker, J. P., and Vietri, M. 1986, ApJ 300, 68.
Ostriker, J. P., and Vietri, M. 1990, Nature 344, 45.
Pascarelle, S. M., Windhorst, R.A., Keel, W. C., and Odewahn, S. C. 1996, Nature 383, 45.
Perlman, E. S., Stocke, J. T., Schachter, J. F., Elvis, M., Ellingson, E., Urry, C. M., Potter, M., Impey, C. D., and Kolchinsky, P. 1996, ApJSuppl 104, 251.
Pettini, M., Smith, L. J., Hunstead, R. W., and King, D. L. 1994, ApJ 426, 79.
Press, W.H., Rybicki, G.B., and Schneider, D.P. 1993, ApJ 414, 64.
Quashnock, J., Vanden Berk, D. E., and York, D. G. 1996, ApJL 472, 69.
Rees, M. 1984, A.R.A.A., 22, 471.
Sanders, D.B., Phinney, E.S., Neugebauer, G., Soifer, B.T., and Mathews, K. 1989, ApJ 347, 29.
Sargent, W. L. W., Young, P. J., Boksenberg, A., and Tytler, D. 1980, ApJSuppl 42, 41.
Schartel, N. et al., 1996a, MNRAS 283, 1015.
Schartel, N., Walter, R., Fink, H. H., and Trümper, J. 1996b, AstrAp 307, 33.
Schmidt, M. 1963, Nature 197, 1040.
Schmidt, M. 1965, ApJ 141, 1295.
Schmidt, M., Schneider, D.P., and Gunn, J.E. 1995, AJ 110, 68.
Schneider, D.P., Schmidt, M., and Gunn, J.E. 1991a, AJ 101, 2001.
Schneider, D.P., Schmidt, M., and Gunn, J.E. 1991b, AJ 102, 837.
Schneider, D.P., Schmidt, M., and Gunn, J.E. 1994, AJ 107, 1245.
Shanks, T., Boyle, B.J., and Peterson, B.A. 1988, in Optical Surveys for Quasars, ASP Conf. Series 2, P.S. Osmer et al. eds. (Brigham Young University: Provo), p. 244.
Shaver, P.A., 1988, in Large Scale Structure of the Universe, IAU Symposium 130, J. Audouze et al. eds., p. 359.
Shaver, P.A., Wall, J.V., Kellerman, K.I., Jackson, C.A., and Hawkins, M.R.S. 1996, Nature 384, 439.
Shull, J. M., Stocke, J. T., and Penton, S. 1996, AJ 111, 72.
Songaila, A. and Cowie, L. 1996, AJ 112, 335.
Steidel, C. C. 1990, ApJSuppl 72, 1.
Steidel, C.C., Dickinson, M., and Persson, S.E. 1994, ApJL 437, 75.
Steidel, C.C., and Sargent, W.L.W. 1991, ApJ 382, 433.
Steidel, C.C., and Sargent, W.L.W. 1992, ApJSuppl 80, 1.
Stocke, J. T., Morris, S. L., Gioia, I. M., Maccacaro, T., Schild, R., Wolter, A., Fleming, T. A., and Henry, J. P. 1991, ApJSuppl 76, 813.
Storrie-Lombardi, L.J., McMahon, R.G., Irwin, M.J., and Hazard, C. 1996, ApJ 468, 121.
Surdej, J., Magain, P., Swings, J.-P., Borgeest, U., Courvoisier, T. J.-L., Kayser, R., Kellerman, K.I., Kuhr, H., and Refsdal, S. 1987, Nature 329, 695.
Tananbaum, H. et al. 1979, ApJLett 234, 9.
Timmes, J. X., Lauroesch, J.T., and Truran, J. 1995, ApJ 451, 468.
Trevese, D., Kron, R.G., Majewski, S.R., Bershady, M.A. and Koo, D.C. 1994, ApJ 433, 494.
Turner, E.L. 1991, AJ 101, 5.
Turner, E.L., Ostriker, J.P., and Gott, J.R. 1984, ApJ 284, 1.
Tytler, D. 1981, Nature 291, 289.
Tytler, D., and Fan, X.M. 1992, ApJSuppl 79, 1.
Tytler, D., and Fan, X.M. 1994, ApJ 424, 87.
Urry, C. M., and Padovani, P. 1995, PASP 107, 803.
Wampler, E.J., Robinson, L.B., and Baldwin, J.A. 1973, Nature 243, 336.
Warren, S.J., and Hewett, P.C. 1990, Rep. Prog. Phys., 53, 1095.
Warren, S.J., Hewett, P.C., Irwin, M.J., McMahon, R.G., Bridgeland, M.T., Bunclark, P.S., and Kibblewhite, E.J. 1987, Nature 325, 131.
Warren, S.J., Hewett, P.C., Osmer, P.S., and Irwin, M.J. 1991a, ApJSuppl 76, 1.
Warren, S.J., Hewett, P.C., and Osmer, P.S. 1991b, ApJSuppl 76, 23.
Warren, S.J., Hewett, P.C., and Osmer, P.S. 1994, ApJ 421, 412.
Webb, J.K., Barcons, X., Carswell, R.F., and Parnell, H.C. 1992, MNRAS 255, 319.
Webster, R.L., Francis, P.J., Peterson, B.A., Drinkwater, M.J., & Masci, F.J. 1995, Nature 375, 469.
Weymann, R., Morris, S. I., Foltz, C. B., and Hewett, P. C. 1991, ApJ 373, 23.
Wisotzki, L., Koehler, T., Groote, D., and Reimers, D. 1996, AstrApSuppl 115, 227.
Wolfe, A.M., Turnshek, D.A., Smith, H.E., and Cohen, R.D. 1986, ApJSuppl 61, 249.
Yanny, B. and York, D.G. 1992, ApJ 391, 569.
Yee, H.K.C., Filippenko, A.V., and Tang, D. 1993, AJ 105, 7.
Yi, I. 1996, ApJ 473, 645.
York, D. G. 1994, in Proceedings of the International School of Physics "Enrico Fermi": Course CXXII, ed: J. Silk and N. Vittorio (Amsterdam: North Holland).
York, D. G., Dopita, M., Green, R. and Bechtold, J. 1986, ApJ 311, 610.